Ultrasonic Flowmeter

 

Basics of Ultrasonic Flow meters

The term ‘ultrasonic’ is used to describe pressure waves at frequencies higher than the human ears can detect.

The velocity of the sound waves in the fluid is the same as the velocity of sound in the fluid. If an ultrasonic beam is transmitted across a pipeline at an angle to the flow direction, the time taken for the pulse to reach the receiver is a function of the flow velocity of the fluid, as well as the velocity of sound in the fluid.

Ultrasonic Flow Meters Working Principle

Ultrasonic flow meters operate using the transit-time differential method. The Transit-time differential measurement is based on a simple physical fact.

Imagine two canoes crossing a river on the same diagonal line, one with the flow and the other against the flow. The canoe moving with the flow needs much less time to reach the opposite bank.

Ultrasonic waves behave exactly the same way. A sound wave travelling in the direction of flow of the product is propagated at a faster rate than one travelling against the flow (vAB > vBA).

Transit times tAB and tBA are measured continuously. The difference (tBA – tAB) in time travelled by the two ultrasonic waves is directly proportional to the mean flow velocity (vm).

Where,

• tAB is Time required for ultrasonic wave to travel from Sensor A to B sensor
• tBA is Time required for ultrasonic wave to travel from Sensor B to A sensor

Thus, this type of flow meter operates on the principle of transit time differences. An acoustic signal (ultrasonic) is transmitted from one sensor to another.

This can be either in the direction of flow (downstream) or against the direction of flow (upstream). The time (transit) that the signal requires to arrive at the receiver is then measured.

According to physical principles, the signal sent against the direction of flow requires longer to return than the signal in the direction of flow.

The difference in the transit time is directly proportional to the velocity of flow.

v ≈ Δ t

v = k Δ t

w here k is a constant

Flow rate is thus, 

Q = v •. A

where,

v = flow velocity

Δt = transit time difference between the signal in the direction of flow and against the direction of flow

Q = volumetric flow

A = pipe cross-sectional area

The mathematical relationship between fluid velocity (v) and the Doppler frequency shift (Δf) is as follows, for fluid velocities much less than the speed of sound through that fluid (v << c):

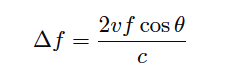
Where,

Δf = Doppler frequency shift

v = Velocity of fluid (actually, of the particle reflecting the sound wave)

f = Frequency of incident sound wave

θ = Angle between transducer and pipe centerlines

c = Speed of sound in the process fluid

Formulas Calculations check here

Transmitter and receiver roles are constantly switched by electronics. Ultrasonic pulses traveling in the direction of the flow, travel path between transducers in a shorter period of time than pulses traveling against the flow.

This is because the flow speeds up pulses traveling downstream but slows down pulses traveling upstream. The equation is;

Multiple traverse Ultrasonic Flow meter

A multiple-transverse configuration consists of two transducers mounted on the pipe so that the signal traverses the fluid two or more times before reaching the other transducer (figure 2). The walls of the pipe reflect the ultrasonic signal in order to maintain at 45 angle.

This allows the signal to remain in the fluid longer, increasing the effective length ( L ) of the signal path, and thus increasing accuracy.

The number of times the signal can traverse through the fluid depends on factors such as transducer frequency, pipe size, pipe wall condition, and the fluid being measured.

Features:

1. Easy to carry;
2. Low maintenance;
3. Can only be used to measure cleaning liquids;
4. Not subject to pipe diameter restrictions;
5. No flow obstruction measurement, no additional pressure loss.

Fluid velocity is measured by sending an ultrasonic pulse from an upstream transducer to a downstream transducer and back again. The measured difference in the amount of time that each pulse takes to traverse the pipe is directly proportional to the mean fluid velocity.

ultrasonic flow meters use this measured velocity to calculate the liquid flow rate based on user-entered information about the process application.

Types of Ultrasonic Flow Meter

Ultrasonic flow meters available in the market are radar, Doppler velocity, ultrasonic clamp-on, and ultrasonic level.

Doppler velocity type meters use reproduced ultrasonic noise to calculate the liquid’s velocity.

Radar type meter employs microwave technology for transmitting small pulses to reflect off a flowing surface back to the sensor for deciding velocity.

Ultrasonic clamp-on type meter is ideal for applications wherever accessing the pipe is difficult otherwise not possible.

Ultrasonic level type meter is ideal for determining the fluid level in both open & closed channels.

Factors Affecting Performance and Accuracy

A. Surface Condition –

Loose or flaking scale, rust, corrosion or dirt on the outside surface of a test piece will interfere with the coupling of sound energy from the transducer into the test material.

Thus, any loose debris of this sort should be cleaned from the specimen with a wire brush or file before measurements are attempted.

Generally it is possible to make corrosion measurements through thin layers of rust, as long as the rust is smooth and well bonded to the metal below.

Some very rough cast or corroded surfaces may have to be filed or sanded smooth in order to insure proper sound coupling. It may also be necessary to remove paint if it has been applied in thick coats, or if it is flaking off the metal.

While it is often possible to make corrosion measurements through thin coats of paint (on the order of a few thousandths of an inch or 0.1 – 0.2mm), thick paint will attenuate signals or possibly create false echoes, causing inaccurate measurements.

Severe pitting on the outside surface of a pipe or tank can be a problem. On some rough surfaces, the use of a gel or grease rather than a liquid couplant will help transmit sound energy into the test piece.

In extreme cases it will be necessary to file or grind the surface sufficiently flat to permit contact with the face of the transducer.

In applications where deep pitting occurs on the outside of a pipe or tank it is usually necessary to measure remaining metal thickness from the base of the pits to the inside wall.

There are sophisticated ultrasonic techniques utilizing focused immersion transducers that can measure directly from the base of the pit to the inside wall, but this is generally not practical for field work.

The conventional technique is to measure unfitted metal thickness ultrasonically, measure pit depth mechanically, and subtract the pit depth from the measured wall thickness.

Alternately, one can file or grind the surface down to the base of the pits and measure nominally.

 

As with any difficult application, experimentation with actual product samples is the best way to determine the limits of a particular gage/transducer combination on a given surface.

B. Transducer Positioning/Alignment –

For proper sound coupling the transducer must be pressed firmly against the test surface.

On small diameter cylindrical surfaces such as pipes, hold the transducer so that the sound barrier material visible on the probe face is aligned perpendicular to the center axis of the pipe.

While firm hand pressure on the transducer is necessary for good readings, the probe should never be scraped along or twisted against a rough metal surface. This will scratch the face of the transducer and eventually degrade performance.

The safest technique for moving a transducer along a rough surface is to pick it up and reposition it for each measurement, not to slide it along.

 

Remember that an ultrasonic test measures thickness at only one point within the beam of the transducer, and that in corrosion situations wall thicknesses often vary considerably.

Test procedures usually call for making a number of measurements within a defined area and establishing a minimum and/or average thickness.

Ideally, data should be taken at increments no greater than half the diameter of the transducer, to insure that no pits or other local variations in wall thickness are missed.

It is possible that on some severely corroded or pitted materials there will be spots where readings cannot be obtained.

This can happen when the inside surface of the material is so irregular that the sound energy is scattered rather than being reflected back to the transducer.

The lack of a reading may also indicate a thickness outside the range of the transducer and instrument being used.

Generally, an inability to obtain a valid thickness reading at a particular point on a test specimen could be a sign of a seriously degraded wall which may warrant investigation by other means.

C. Calibration –

The accuracy of measurements are only as good as the accuracy and care with which the gauge has been calibrated.

It is essential that the velocity and zero calibrations be performed whenever the transducer is changed or you have a reason to doubt the accuracy of the readings.

Periodic checks with samples of known thicknesses are recommended to verify that the gauge is operating properly.

D. Taper or Eccentricity –

If the contact surface and the back surface are tapered or eccentric with respect to each other, the return echo again becomes distorted and the accuracy of measurement is diminished.

E. Acoustic Properties of the Material –

There are several conditions found in engineering materials that can severely limit the accuracy and thickness range that can be measured.

1. “ Sound Scattering ” –

In some materials, notably certain types of cast stainless steel, cast irons, and composites, the sound energy is scattered from individual crystallites in the casting or from dissimilar materials within the composite.

This effect reduces the ability to discriminate a valid return echo from the back side of the material and limits the ability to gauge the material ultrasonically.

2. Velocity Variations –

A number of materials exhibit significant variations in sound velocity from point-to-point within the material.

Certain types of cast stainless steels and brass exhibit this effect due to a relatively large grain size and the anisotropy of sound velocity with respect to grain orientation.

Other materials show a rapid change in sound velocity with temperature. This is characteristic of plastic materials where temperature must be controlled in order to obtain maximum precision in the measurement.

3. Sound Attenuation or Absorption –

In many organic materials, such as low density plastics and rubber, sound is attenuated very rapidly at the frequencies used in normal ultrasonic thickness gauging.

Therefore, the maximum thickness that can be measured in these materials is often limited by sound attenuation.

Pros and Cons of Ultrasonic Flow Meters

Advantages of Ultrasonic Flow Meter

The advantages are

It does not block the path of liquid flow.

The o/p of this meter is different for density, viscosity & temperature of the liquid.

The flow of liquid is bidirectional

The dynamic response of this meter is good.

The output of this meter is in analog form

Conservation of energy

It is appropriate for huge quality flow measurement

It is handy to fit and maintain

Versatility is good

There is no contact to liquid

There is no leakage risk

There are no moving parts, pressure loss

High accuracy

Disadvantages of Ultrasonic Flow Meter

The disadvantages are

It is expensive as compared with other mechanical flow meters.

Design of this meter is complex

Auditory parts of this meter are expensive.

These meters are complicated as compared with other meters, thus it requires specialists for maintaining and repairing these meters

It cannot measure cement or concrete pipes one they rusted.

It doesn’t work once the pipe contains holes or bubbles in it

Can’t measure cement/concrete pipe or pipe with such material lining

Applications

The applications of ultrasonic flow meters include the following.

These meters are used in wastewater and dirty liquid applications

These meters are used wherever chemical compatibility, less maintenance, and low-pressure drop are required.

These meters are used to measure the velocity of a liquid through ultrasound to analyze volume flow.

These meters measure the disparity between the transit time of ultrasonic pulses which transmits with the direction of liquid flow

The applications of these meters range from process to custody flow

This is one kind of device for volumetric flow measurement for liquids as well as gases.

These are excellent alternatives for both vortex & electromagnetic flowmeters.

The difference in the transit time is directly proportional to the velocity of flow.

v ≈ Δ t

v = k Δ t

w here k is a constant

Flow rate is thus, 

Q = v •. A

where,

v = flow velocity

Δt = transit time difference between the signal in the direction of flow and against the direction of flow

Q = volumetric flow

A = pipe cross-sectional area

The mathematical relationship between fluid velocity (v) and the Doppler frequency shift (Δf) is as follows, for fluid velocities much less than the speed of sound through that fluid (v << c):

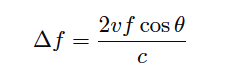
Where,

Δf = Doppler frequency shift

v = Velocity of fluid (actually, of the particle reflecting the sound wave)

f = Frequency of incident sound wave

θ = Angle between transducer and pipe centerlines

c = Speed of sound in the process fluid

Note how the Doppler effect yields a direct measurement of fluid velocity from each echo received by the transducer.

This stands in marked contrast to measurements of distance based on time-off light (time domain reflectometry – where the amount of time between the incident pulse and the returned echo is proportional to distance between the transducer and the reflecting surface)

such as in the application of ultrasonic liquid level measurement. In a Doppler flowmeter, the time delay between the incident and reflected pulses is irrelevant. Only the frequency shift between the incident and reflected signals matters.

This frequency shift is also directly proportional to the velocity of flow, making the Doppler ultrasonic flowmeter a linear measurement device.

Re-arranging the Doppler frequency shift equation to solve for velocity (again, assuming v << c)

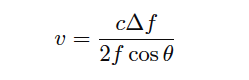
Knowing that volumetric flow rate is equal to the product of pipe area and the average velocity of the fluid (Q = Av), we may re-write the equation to directly solve for calculated flow rate (Q):

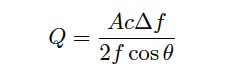
A very important consideration for Doppler ultrasonic flow measurement is that the calibration of the flow meter varies with the speed of sound through the fluid (c).

This is readily apparent by the presence of c in the above equation: as c increases, Δf must proportionately decrease for any fixed volumetric flow rate Q.

Since the flowmeter is designed to directly interpret flow rate in terms of Δf, an increase in c causing a decrease in Δf will thus register as a decrease in Q.

This means the speed of sound for a fluid must be precisely known in order for a Doppler ultrasonic flowmeter to accurately measure flow.

The speed of sound through any fluid is a function of that medium’s density and bulk modulus (how easily it compresses):

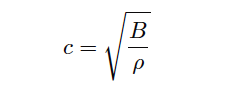
Where,

c = speed of sound in a material (meters per second)

B = Bulk modulus (pascals, or newtons per square meter)

ρ = Mass density of fluid (kilograms per cubic meter)

Temperature affects liquid density, and composition (the chemical constituency of the liquid) affects bulk modulus. Thus, temperature and composition both are influencing factors for Doppler ultrasonic flowmeter calibration.

Pressure is not a concern here, since pressure only affects the density of gases, and we already know Doppler flowmeters only function with liquids.

Following on the theme of requiring bubbles or particles of sufficient size, another limitation of Doppler ultrasonic flowmeters is their inability to measure flow rates of liquids that are too clean and too homogeneous. In such applications, the sound-wave reflections will be too weak to reliably measure.

Such is also the case when the solid particles have a speed of sound too close to the that of the liquid, since reflection happens only when a sound wave encounters a material with a markedly different speed of sound.

Doppler-type ultrasonic flowmeters are useless in applications where we cannot obtain strong sound-wave reflections.

Transit-time flowmeters, sometimes called counterpropagation flowmeters, are an alternative to Doppler ultrasonic flowmeters.

A transit-time ultrasonic flowmeter uses a pair of opposed sensors to measure the time difference between a sound pulse traveling with the fluid flow versus a sound pulse traveling against the fluid flow.

Since the motion of fluid tends to carry a sound wave along, the sound pulse transmitted downstream will make the journey faster than a sound pulse transmitted upstream:

Transit-time flow meters

The rate of volumetric flow through a transit-time flowmeter is a simple function of the upstream and downstream propagation times:

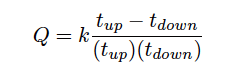
Where,

Q = Calculated volumetric flow rate

k = Constant of proportionality

tup = Time for sound pulse to travel from downstream location to upstream location (upstream, against the flow)

tdown = Time for sound pulse to travel from upstream location to downstream location (downstream, with the flow)

An interesting characteristic of transit-time velocity measurement is that the ratio of transit time difference over transit time product remains constant with changes in the speed of sound through the fluid.

If you would like to prove this to yourself, you may do so by substituting path length (L), fluid velocity (v), and sound velocity (c) for the times in the flow formula. Use tup = L/(c−v) and tdown = L/(c+v) as your substitutions, then algebraically reduce the flow formula until you find that all the c terms cancel. Your final result should be Q = 2kv/L .

When this equation is cast into terms of path length (L), fluid velocity (v), and sound velocity (c), the equation simplifies to Q = 2kv/L , proving that the transit-time flow meter is linear just like the Doppler flowmeter, with the advantage of being immune to changes in the fluid’s speed of sound.

Changes in bulk modulus resulting from changes in fluid composition, or changes in density resulting from compositional, temperature, or pressure variations therefore have little effect on a transit-time flow meter’s accuracy.

Not only are transit-time ultrasonic flow meters immune to changes in the speed of sound, but they are also able to measure that sonic velocity independent of the flow rate.

The equation for calculating speed of sound based on upstream and downstream propagation times is as follows:

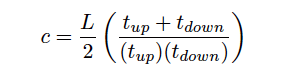
Where,

c = Calculated speed of sound in fluid

L = Path length

tup = Time for sound pulse to travel from downstream location to upstream location (upstream, against the flow)

tdown = Time for sound pulse to travel from upstream location to downstream location (downstream, with the flow)

While not necessary or even particularly relevant for the direct purpose of flow measurement, this inference of the fluid’s speed of sound is nevertheless useful as a diagnostic tool. If the true speed of sound for the fluid is known either by direct laboratory measurement of a sample or by chemical analysis of a sample, this speed may be compared against the flow meter’s reported speed of sound to check the flow meter’s absolute transit time measurement accuracy. Certain problems within the sensors or within the sensor electronics may be detected in this way.

A requirement for reliable operation of a transit-time ultrasonic flow meter is that the process fluid be free from gas bubbles or solid particles which might scatter or obstruct the sound waves.

Note that this is precisely the opposite requirement of Doppler ultrasonic flow meters, which require bubbles or particles to reflect sound waves.

These opposing requirements neatly distinguish applications suitable for transit-time flow meters from applications suitable for Doppler flow meters, and also raise the possibility of using transit-time ultrasonic flow meters on gas flow streams as well as on liquid flow streams.

One potential problem with any ultrasonic flow meter is being able to measure the true average fluid velocity when the flow profile changes with Reynolds number. If just one ultrasonic “beam” is used to probe the fluid velocity, the path this beam takes will likely see a different velocity profile as the flow rate changes (and the Reynolds number changes along with it).

Recall the difference in fluid velocity profiles between low Reynolds number flows (left) and high Reynolds number flows (right):

A popular way to mitigate this problem is to use multiple sensor pairs, sending acoustic signals along multiple paths through the fluid (i.e. a multipath ultrasonic flowmeter), and to average the resulting velocity measurements.

Dual-beam transit-time flow meters have been in use for well over a decade at the time of this writing (2009), and one manufacturer even has a five beam ultrasonic flowmeter model which they claim maintains an accuracy of ± 0.15% through the laminar-to-turbulent flow regime transition.

4 Channel ultrasonic flow meter

A simplified illustration of a Daniel four-beam (or four “chord”) ultrasonic flowmeter is shown here:

Multipath ultrasonic flowmeters, by virtue of measuring more than one sound wave path through the fluid, also have the ability to detect irregular flow profiles.

Each sonic path between sensor pairs in a transit-time ultrasonic flow meter, called a chord, measures flow velocity. The velocities reported for each chord may be compared to the flow meter’s calculated average flow velocity, and expressed as velocity ratios.

A particular chord measuring a velocity greater than the flow meter’s average will report a velocity ratio greater than one (> 1), whereas a chord measuring a velocity less than the meter’s average will report a velocity ratio less than one (< 1).

In the Daniel four-chord ultrasonic flow meter, two chords (B and C) measure velocity near the center of the pipe while the others (A and D) measure velocity closer to the pipe walls.

 

In normal operation, the center chord velocity ratios should exceed the outer chord velocity ratios by a small amount, since the flow profiles of laminar and turbulent flow regimes alike exhibit a greater velocity at the center of a pipe than near the walls of a pipe.

Another parameter called profile factor expresses the chord velocity factors as a ratio, inner velocity factors over outer velocity factors: (B+C)/(A+D), a number which should always exceed one (> 1).

The exact value of this profile factor varies with the flow meter’s installation, and may shift over time if the flow profile shifts for some reason (e.g. partial blockage in a flow conditioner, piping change, accumulation of debris on pipe wall).

For example, a pipe accumulating dirt or other solid material on its walls over time will tend to slow down the velocity of fluid near the walls compared to the velocity of fluid in the center. This has the effect of decreasing chord A and D velocity ratios while increasing chord B and C velocity ratios, which in turn increases the profile factor value.

In this regard, the profile factor value for an operating flowmeter may be an important diagnostic tool, indicating some physical abnormality within the piping.

As previously mentioned, it is possible for a transit-time ultrasonic flowmeter to measure the speed of sound through the fluid from the sum of the upstream and downstream transit times.

Multipath transit-time flowmeters may use this feature to cross-check calculated speed of sound values measured by each chord, as a self-diagnostic tool.

Since each chord measures the same gas composition, each chord’s calculated speed of sound should be exactly equal. Significant differences in calculated speed of sound between chords suggests a failure in the acoustic sensor(s) or electronics for the errant chord.

Some modern ultrasonic flowmeters have the ability to switch back and forth between Doppler and transit-time (counterpropagation) modes, automatically adapting to the fluid being sensed. This capability enhances the suitability of ultrasonic flowmeters to a wider range of process applications.

Ultrasonic flowmeters are adversely affected by swirl and other large-scale fluid disturbances, and as such may require substantial lengths of straight pipe upstream and downstream of the measurement flowtube to stabilize the flow profile.

 

Like magnetic flowmeters, ultrasonic flowmeters are completely non-obstructive, which means they exhibit extremely low permanent pressure loss and will not accumulate debris.

Advances in ultrasonic flow measurement technology have reached a point where it is now feasible to consider ultrasonic flowmeters for custody transfer measurement of natural gas.

The American Gas Association has released a report specifying the use of multipath transit-time ultrasonic flowmeters in this capacity (Report #9). As with the AGA’s #3 (orifice plate) and #7 (turbine) high-accuracy gas flow measurement standards, the AGA9 standard requires the addition of pressure and temperature instruments on the gas line to measure gas pressure and temperature in order to calculate flow either in units of mass or in units of standardized volume (e.g. SCFM).

The measurement of temperature and pressure for a transit-time ultrasonic flowmeter has nothing to do with correcting errors within the meter itself, since we know transit-time flowmeters are inherently immune to changes in gas density or composition.

Temperature and pressure measurements are necessary for custody transfer applications simply because ultrasonic flowmeters, like turbine flowmeters, measure only volumetric flow.

The fair sale and purchase of a gas requires measurement of molecular quantity, not just volume, which is why a flow computer requires measurements of pressure and temperature in order to convert the ultrasonic flowmeter’s volumetric output to either mass flow or standardized volumetric flow.

A unique advantage of ultrasonic flow measurement is the ability to measure flow through the use of temporary clamp-on sensors rather than a specialized flow tube with built-in ultrasonic transducers. While clamp-on sensors are not without their share of problems, they constitute an excellent solution for certain flow measurement applications.

An important criterion for successful application of a clamp-on flow meter is that the pipe material be homogeneous in nature, to efficiently conduct sound waves between the process fluid and the clamp-on transducers. Porous pipe materials such as clay and concrete are therefore unsuitable for clamp-on ultrasonic flow measurement.

Thanks for reading - Ultrasonic Flow meter
Naitik Patel
Industrial Guide