Coriolis Mass Flow Meter

Coriolis ﬂow meters represent the state-of-the-art in mass ﬂow measurement. While incredibly versatile and accurate, their internal operation can be diﬃcult to understand.

Coriolis Flow Meters

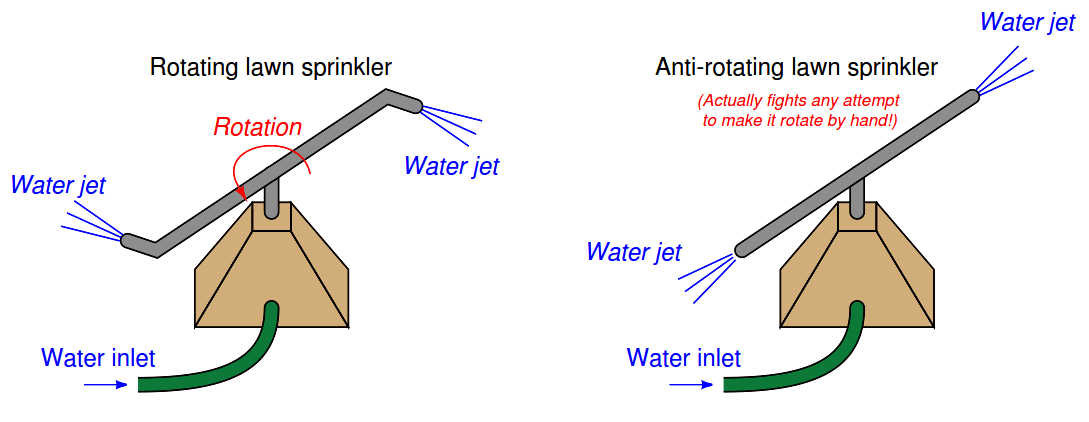
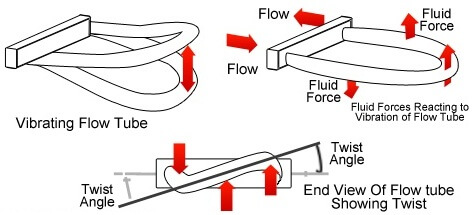
Put into very simple terms, a Coriolis ﬂow meter works by shaking one or more tubes carrying the ﬂowing ﬂuid, then precisely measuring the frequency and phase of that shaking.

The back-and-forth shaking is driven by an electromagnetic coil, powered by an electronic ampliﬁer circuit to shake the tube(s) at their mechanical resonant frequency.

Since this frequency depends on the mass of each tube, and the mass of the tubes depends on the density of the ﬂuid ﬁlling the ﬁxed volume of the tubes, the resonant frequency becomes an inverse indication of ﬂuid density (Note 1) , whether or not ﬂuid is ﬂowing through the tubes.

As ﬂuid begins to move through the tubes, the inertia of the moving ﬂuid adds another dimension to the tubes’ motion: the tubes begin to undulate (Note 2) , twisting slightly instead of just shaking back and forth.

This twisting motion is directly proportional to the mass ﬂow rate, and is internally measured by comparing the phase shift (θ) between motion at one point on the tube versus another point on the tube: the greater the undulation, the greater the phase shift between these two points’ vibrations.

Note 1: In fact, this density-measuring function of Coriolis ﬂow meters is so precise that they often ﬁnd use primarily as density meters, and only secondarily as ﬂow meters!

Note 2 : An interesting experiment to perform consists of holding a water hose in a U-shape and gently swinging the hose back and forth like a pendulum, then ﬂowing water through that same hose while you continue to swing it. The hose will begin to undulate, its twisting motion becoming visually apparent.

Coriolis ﬂow meters formula

The Coriolis force

In physics, certain types of forces are classiﬁed as ﬁctitious or pseudo forces because they only appear to exist when viewed from an accelerating perspective (called a non-inertial reference frame).

The feeling you get in your stomach when you accelerate either up or down in an elevator, or when riding a roller-coaster at an amusement park, feels like a force acting against your body when it is really nothing more than the reaction of your body’s inertia to being accelerated by the vehicle you are in.

The real force is the force of the vehicle against your body, causing it to accelerate. What you perceive is merely a reaction to that force, and not the primary cause of your discomfort as it might appear to be.

Centrifugal force is another example of a “pseudo force” because although it may appear to be a real force acting on any rotating object, it is in fact nothing more than an inertial reaction.

Centrifugal force is a common experience to any child who has ever played on a “merry-go-round:” that perception of a force drawing you away from the center of rotation, toward the rim.

The real force acting on any rotating object is toward the center of rotation (a centripetal force) which is necessary to make the object radially accelerate toward a center point rather than travel in a straight line as it normally would without any forces acting upon it. When viewed from the perspective of the spinning object, however, it would seem there is a force drawing the object away from the center (a centrifugal force).

Yet another example of a “pseudo force” is the Coriolis force, more complicated than centrifugal force, arising from motion perpendicular to the axis of rotation in a non-inertial reference frame.

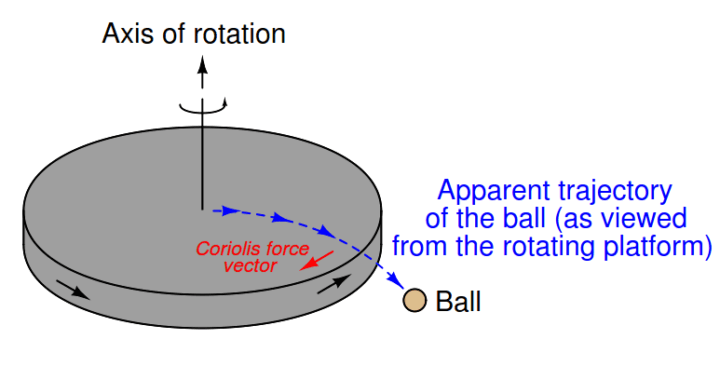
The example of a merry-go-round works to illustrate Coriolis force as well: imagine sitting at the center of a spinning merry-go-round, holding a ball. If you gently toss the ball away from you and watch the trajectory of the ball, you will notice it curve rather than travel away in a straight line.

In reality, the ball is traveling in a straight line (as viewed from an observer standing on the ground), but from your perspective on the merry-go-round, it appears to be deﬂected by an invisible force which we call the Coriolis force.

In order to generate a Coriolis force, we must have a mass moving at a velocity perpendicular to an axis of rotation:

The magnitude of this force is predicted by the following vector equation :

Coriolis ﬂow meters equation

If we replace the ball with a ﬂuid moving through a tube, and we introduce a rotation vector by tilting that tube around a stationary axis (a fulcrum), a Coriolis force develops on the tube in such a way as to oppose the direction of rotation just like the Coriolis force opposed the direction of rotation of the rotating platform in the previous illustration:

To phrase this in anthropomorphic terms, the ﬂuid “ﬁghts” against this rotation because it “wants” to keep traveling in a straight line.

For any given rotational velocity, the amount of “ﬁght” will be directly proportional to the product of ﬂuid velocity and ﬂuid mass. In other words, the magnitude of the Coriolis force will be in direct proportion to the ﬂuid’s mass ﬂow rate. This is the basis of a Coriolis mass ﬂowmeter.

A demonstration of this Coriolis force may be made by modifying the nozzles on a rotary lawn sprinkler so they point straight out from the center rather than angle in one direction. As water squirts through the now-straight nozzles, they no longer generate a rotational reaction force to spin the nozzle assembly, and so the nozzles remain in place (this much should be obvious).

However, if someone were to try rotating the nozzle assembly by hand, they would discover the Coriolis force opposes the rotation, acting to keep the nozzle assembly from rotating.

The greater the mass ﬂow rate of water through the nozzles, the stronger the inhibiting Coriolis force. Instead of a rotating lawn sprinkler, you are now the proud owner of an anti-rotating lawn sprinkler that actually ﬁghts any attempt to rotate it:

This is a very non-intuitive concept, so it deserves further explanation. The “anti-rotating” sprinkler doesn’t just fail to rotate on its own – it actually opposes any attempt to rotate from an external force (e.g. a person trying to push the tubes by hand).

This opposition would not occur if the tubes were merely capped oﬀ at the ends and ﬁlled with stagnant water. If this were the case, the tubes would simply be heavy with the water’s weight, and they would rotate freely about the axis just like any pair of heavy metal tubes would (whether hollow and ﬁlled with water, or solid metal).

The tubes would have inertia, but they would not actively oppose any external eﬀort to rotate.

Having liquid water move through the tubes is what makes the diﬀerence, and the reason becomes clear once we imagine what each water molecule experiences as it ﬂows from the center (axis of rotation) to the nozzle at the tube tip.

Each water molecule originating from the center begins with no lateral velocity, but must accelerate as it travels farther along the tube toward the circumference of the tips’ rotation where the lateral velocity is at a maximum.

The fact that new water molecules are continually making this journey from center to tip means there will always be a new set of water molecules requiring acceleration from center velocity (zero) to tip velocity (maximum).

In capped tubes ﬁlled with stagnant water, the acceleration would only occur in getting the tubes’ rotation up to speed – once there, the lateral velocity of each water molecule sitting stagnant inside the tubes would remain the same.

However, with water ﬂowing from center to tip, this process of acceleration from zero velocity to tip velocity must occur over and over again (continually) for each new water molecule ﬂowing through. This continual acceleration of new mass is what generates the Coriolis force, and what actively opposes any external force trying to rotate the “anti-rotating” sprinkler.

As you might guess, it can be diﬃcult to engineer a tubing system capable of spinning in circles while carrying a ﬂow stream of pressurized ﬂuid.

To bypass the practical diﬃculties of building a spinning tube system, Coriolis ﬂow meters are instead built on the principle of a ﬂexible tube that oscillates back and forth, producing the same eﬀect in a cyclic rather than continuous fashion. The eﬀect is not unlike shaking a hose (Note) side to side as it carries a stream of water:

Note : The Coriolis force generated by a ﬂowing ﬁre hose as ﬁreﬁghters work to point it in a diﬀerent direction can be quite signiﬁcant, owing to the high mass ﬂow rate of the water as it ﬂows through the hose and out the nozzle!

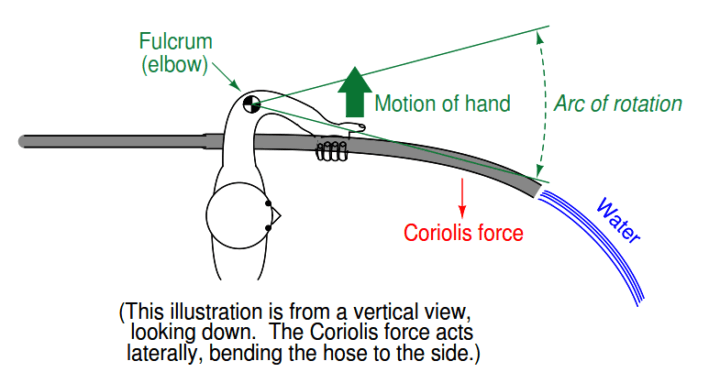
The Coriolis force opposes the direction of rotation. The greater the mass ﬂow rate of water through the hose, the stronger the Coriolis force.

If we had a way to precisely measure the Coriolis force imparted to the hose by the water stream, and to precisely wave the hose so its rotational velocity held constant for every wave, we could directly infer the water’s mass ﬂow rate.

Mass flow meters are the types of flow meters which are mainly employed in mass-related processes such as chemical reactions, heat transfer, etc. In all these processes, accurate measurement of flow is the prerequisite.
There are numerous types of mass flow meters available in the industry. However, the most widely used type is the Coriolis meter. Another type available is thermal type mass flow meters
Coriolis Mass Flow Meter
A Coriolis meter works on Coriolis Effect, hence it is named so. Coriolis meters are considered to be true mass meters since they tend to measure the mass rate of flow directly while other flow meter technologies measure volumetric flow.

Since mass does not change, no adjustments are needed for varying fluid characteristics. Hence, a Coriolis meter operates in linear fashion.

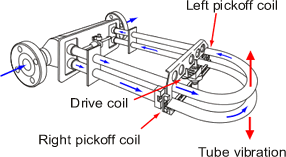
These types of meters exist in variety of designs.
The most common type of unit includes
U-shaped flow tube
Sensor assembly
Electronics unit
In this meter unit, the liquid passes through a U-shaped tube which vibrates in an angular harmonic oscillation. Coriolis forces will then deform the tube and a further vibration component gets added to the already oscillating tube. This added vibration element results in a phase shift or twist in few parts of the tubes.

This resulting phase shift which is directly proportional to the liquid mass flow rate is measured with the help of sensors. This measured information is further transferred to the electronics unit where it gets transformed to a voltage proportional to mass flow rate. A Coriolis meter is shown in the figure below:

Principal of Operation

The flow is guided into the U-shaped tube. When an oscillating excitation force is applied to the tube causing it to vibrate, the fluid flowing through the tube will induce a rotation or twist to the tube because of the Coriolis acceleration acting in opposite directions on either side of the applied force.
For example, when the tube is moving upward during the first half of a cycle, the fluid flowing into the meter resists being forced up by pushing down on the tube. On the opposite side, the liquid flowing out of the meter resists having its vertical motion decreased by pushing up on the tube.
This action causes the tube to twist. When the tube is moving downward during the second half of the vibration cycle, it twists in the opposite direction.

This twist results in a phase difference (time lag) between the inlet side and the outlet side and this phase difference is directly affected by the mass passing through the tube.

An advantage of Coriolis flow meters is that it measures the mass flow rate directly which eliminates the need to compensate for changing temperature, viscosity, and pressure conditions.

A more recent single straight tube design is available to measure some dirty and/or abrasive liquids that may clog the older U-shaped design.

For working properly, a minimum gas density of 4.5 kg/m3 is required. (Changes from vendor to vendor)
Theoretically, Coriolis force,
**Fc= 2mw*V**
m= mass (kg)
w= angular velocity (rad/s)

V= velocity (m/s)
‘U’ and ‘Ω’ shaped coriolis meters cause pressure drop as the flow is increased, resulting in permanent pressure loss.
Consequently, liquids near boiling point could introduced cavitation as the pressure across the meter drops below the vapour pressure of the liquid (forming of vapour bubbles).
As soon as the pressure recovers above the vapour pressure the bubbles impode.
Cavitation will cause the meter to malfunction and this should be avoided at all times.
The cross-section of the tube is normally smaller than the cross-section of the line pipe to increase the velocity (v) in order to create higher Coriolis forces. The latter holds good for Coriolis meters with straight measuring tubes as well. Consequently, the pressure drop will increase accordingly.

Coriolis mass flow meters will measure the mass flow rate and actual density accurately irrespective of the nature of the fluid as long as the flow is single phase and the fluid is homogeneous.
Being accurate, they are often used for custody transfer and critical reactor feed (ratio) control and also in streams where large variation in fluid composition will occur, which otherwise could not be measured.
A weak point is their requirement for Zero Adjustment at operation conditions. the zero adjustment is easily upset by not fully stress free installation of the meter.
The importance of zero adjustment is also demonstrated in the formula for the uncertainty in the reading of the meter, expressed as:
+/-[(zero stability/ flow rate)*100]% +/- x%
where x varies between 0.1 and 0.3% depending on design of the meter.

Coriolis Mass Flow Meter Main Features Advantages Disadvantages explained in this blog

Main Features

A Coriolis meter can be applied for variety of applications ranging from adhesives and coatings to liquid nitrogen.
Typical rangeability of curved tube designed Coriolis meters vary from 100:1 to 200:1 whereas for straight-tube meters its rangeability is limited i.e. about 30:1 to 50:1. Besides, accuracy of straight tube meters is low.
In case of Coriolis meters, no compensation is needed for temperature and pressure variations. Also mass measurement is insensitive to changes in viscosity and density.

They are particularly helpful for handling liquids whose viscosity changes according to velocity while temperature and pressure remains constant.
These are called universal meters, since they are capable enough to measure nearly all liquids, slurries and gases. They can measure all liquid flows such as Newtonian, non-Newtonian and moderately dense gases as well.
They can be employed to measure liquid density also.
No Reynolds number restrictions are allied with Coriolis flow meters.
They are also not affected by deformations in velocity profile.

The advantages & limitations of Coriolis flow meter are:

Advantages of Coriolis Meters

Coriolis flow meter is capable of measuring a wide range of fluids that are often incompatible with other flow measurement devices. The operation of the flow meter is independent of Reynolds number; therefore, extremely vicious fluids can also be measured. A Coriolis flow meter can measure the flow rate of Newtonian fluids, all types’ non-Newtonian fluids, and slurries. Compressed gases and cryogenic liquids can also be measured by some designs.
Coriolis flow meters provide a direct mass flow measurement without the addition of external measurement instruments. While the volumetric flow rate of the fluid will vary with changes in density, the mass flow rate of fluid is independent of density changes.
Coriolis flow meters have outstanding accuracy. The base accuracy is commonly on the order of 0.2%. In addition, the flow meters are linear over their entire flow range.

The rangeability of flow meters is usually on the order of 20:1 or greater. Coriolis flow meters have been successfully applied at flow rates 100 times lower than their full scale flow rate.
A Coriolis flow meter is capable of measuring mass flow rate, volumetric flow rate, fluid density and temperature — all from one instrument.
The operation of the flow meter is independent flow characteristics such as turbulence and profile. Therefore, upstream and downstream straight run requirement and flow conditioning are not necessary. They can also be used in installations that have pulsating flow.
Coriolis flow meters do not have internal obstructions witch can be damaged or plugged by slurries or other types of particulate matter in the flow stream. Entrained gas or slugs of gas in the liquid will not damage the flow meter. There are no moving parts witch will wear out require replacement. These design features reduces the need for routine maintenance.
The flow meter can be configured to measure flow in either the forward or the reverse direction. In revere flow there will still be a time or phase difference between the flow detector, but the relative difference between the two detector signals will be reversed.
Coriolis flow meter designs are available witch allow for use in sanitary applications, and for the measurement of shear sensitive fluids. Materials are available to permit the measurement of corrosive fluids.

Disadvantages of Coriolis Meters

Coriolis flow meters are not available for large pipelines. The largest Coriolis flow meter that is currently available has a maximum flow rating of 25,000 lb/min (11,340 kg/min), and is equipped with 6 in. (15 cm) flanges. When larger flow rates must be measured, two or more flow meters mounted in parallel are required.
Some flow meter designs require extremely high fluid velocities in order to achieve a significant amount of time or phase difference between the flow detector signals. This can result in extremely high pressure drops across the flow meter.

Coriolis flow meters are expensive. However, the cost of a Coriolis meter is often comparable to (or below) the cost of a volumetric meter plus densitometer used together to determine the mass flow rate.
Coriolis flow meters have difficulty measuring the flow rate of low- pressure gas. Application with pressure less than 150 psig are marginal with the flow meter designs that are currently available. Low-pressure gases have low density, and their mass flow rate is usually very low.
In order to generate enough mass flow rates to provide sufficient Coriolis force to be measured, the gas velocity must be extremely high. This in turn may lead to prohibitively high pressure drops across the meter.

Industrial Guide Pro